
That’s our final answer: The volume of the given triangular prism equals 510 feet cubed. When we multiply feet by feet by feet and when we’re discussing volume, we know that our units will be cubed. And 30 times 17 equals 510.īut we’re not finished here because we need to decide what to do with our units. Step 3: Once the value of the volume of the prism is obtained, write the unit of volume of prism in the end (in terms of cubic units). Step 2: Find the volume of the prism using the formula V B × H where V, B, and H are the volume, base area, and height of the prism. The volume of Triangular Pyramid For knowing the volume of the triangular pyramid, multiply the area of the triangular base with the height of the pyramid and then divide the number by 3. Then we multiply the area of our base by the height of our prism, 17 feet. Step 1: First write the given dimensions of the prism. The volume formula for a triangular prism is (height x base x length) / 2, as seen in the figure below: So, you need to know just three measures: height. For our base, our triangle, one-half times six times 10. Let’s start plugging things into our formula. And the height of our triangular prism is 17 feet. So we see, in our case, the base of our triangle is 10 feet and the height of our triangle is six feet. It’s the distance from one base to the other.Īnd how do we go about finding the area of the base? Well, like any triangle, we multiply one-half, the base of that triangle, times the height of that triangle. And the green portion represents the height. The volume is then the area of the base multiplied by the height. Here is another way to visualize a triangular prism. The volume of a triangular prism can be found by multiplying the base times the height, where the shaded pink portion represents the base. Develop and use a formula to find the volume of a right triangular prism.


It should not be confused with a pyramid.
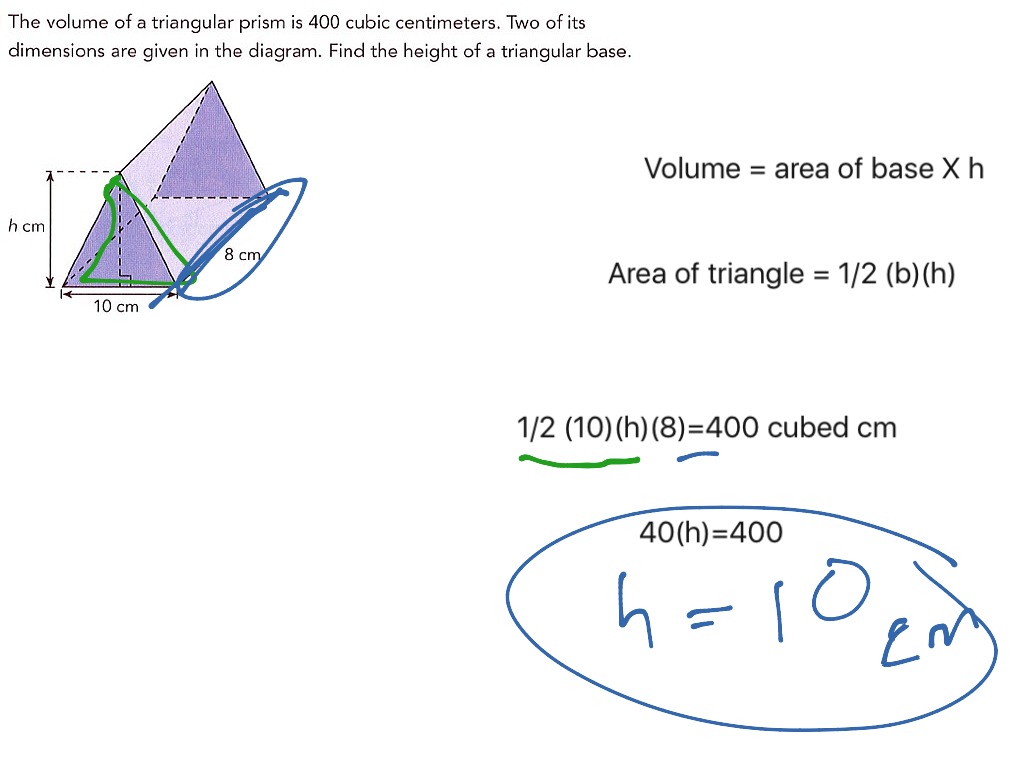
Determine the volume of the given triangular prism. A triangular prism is a three-sided polyhedron with two parallel triangular bases and three rectangular faces.


 0 kommentar(er)
0 kommentar(er)
